In order to rationally create an inducible lysis system, we modeled the dynamics of the lysis of the cells under two different inducers: one induced by arabinose and another induced by quorum sensing mechanisms.
Arabinose inducible system model:
Equations:
With our model, we assumed that with a constant presence of arabinose, there would be a constant transcription rate β of the T4 lysis mRNA transcript. Additionally, because the T4 lysis protein works by creating holes in the membrane of the bacteria, there would exist a certain threshold where enough holes would cause the cells to lyse, where this threshold is modeled by the K term and the hill function for the T4 protein concentration. All other terms are modeled to exhibit first order kinetics in terms of the appropriate reactants. The differential equations used for this system are shown below:
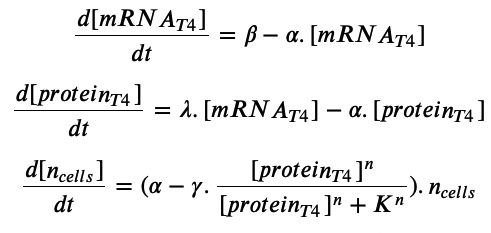
Plots:
The above differential equations can be simulated to generate the following graphs.
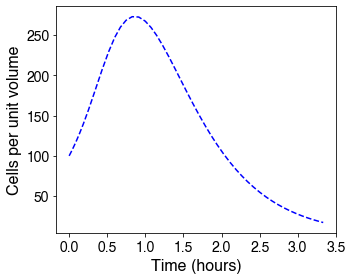
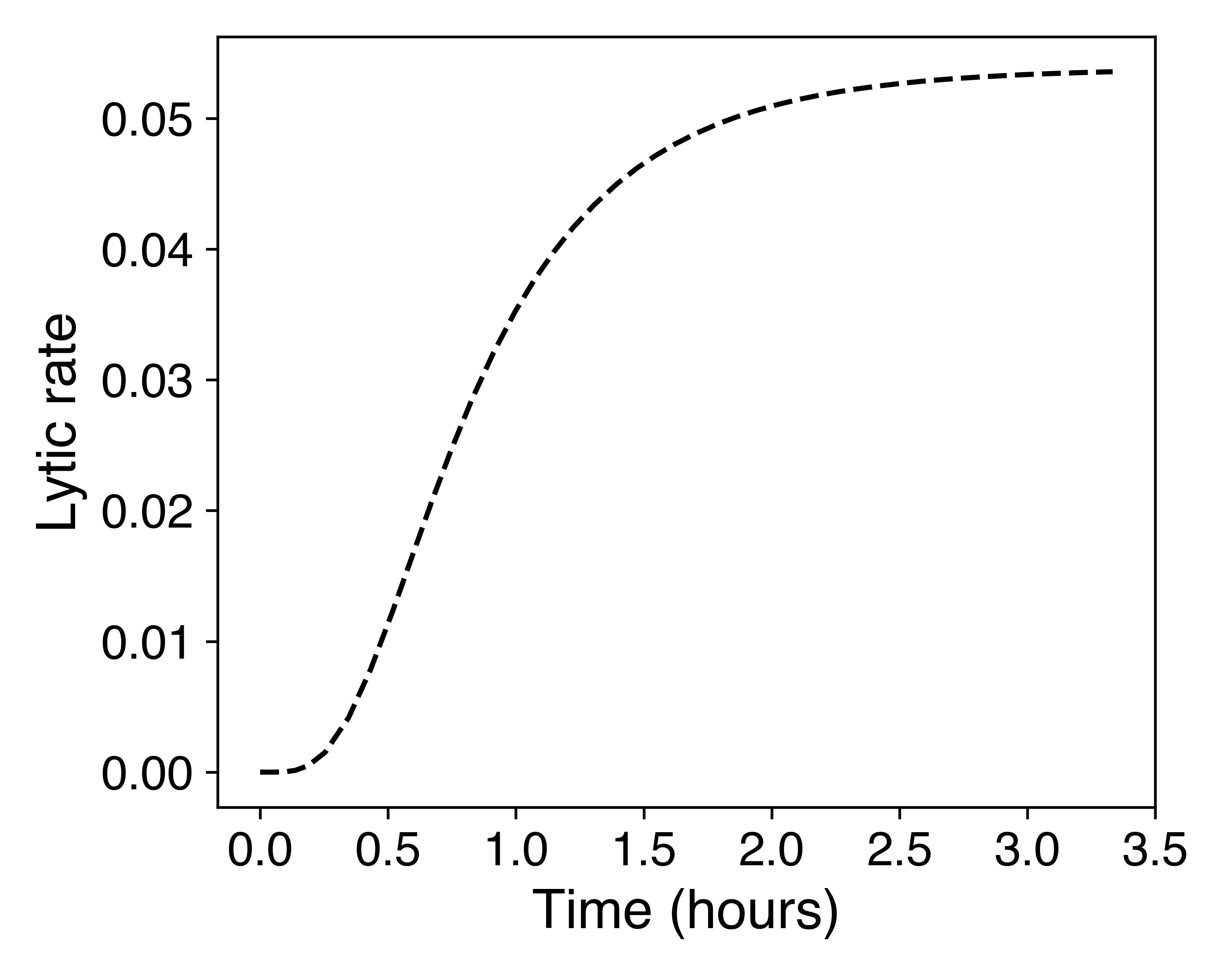
Based on the graphs, we see that there is an initial delay in lysis, where the cells are still growing until they reach a peak in their concentration, after which the concentration falls once the lytic rate passes a certain threshold. This delay matches the experimental data demonstrated in the contribution section, therefore demonstrating the model as an accurate representation of the data. This accurately predicted delay provides flexibility in the ATPS design: even with arabinose induction, there is still enough time to place the bacteria in protocells and for them to grow before they lyse.
Quorum Sensing system model:
As discussed in the integrated human practices, we received the feedback that the quorum sensing induction of the lysis system would be beneficial to obtain a high concentration of bacterial cells within the droplets before lysis occurs. Therefore, building on the arabinose-induction model as a proof of concept, we went on to construct a model of the quorum sensing system.
Equations:
In the quorum sensing system, the downstream gene is promoted when the molecule AHL released by E. coli binds to a transcription factor and binds to the pLuxR promoter. In our proposed genetic circuit, we have implemented a positive feedback mechanism: both the T4 lysis gene and the LuxI gene that generates AHL are under regulation of the pLuxR promoter. In this way, the positive feedback regulation would create a delay-switch like response once enough AHL has been accumulated due to a high enough local concentration of E. coli. This switch like behavior is encoded in the Michaelis Menten term for the mRNA transcripts for the T4 gene and the LuxI gene, and all other terms follow similar kinetics as before.

Plots:
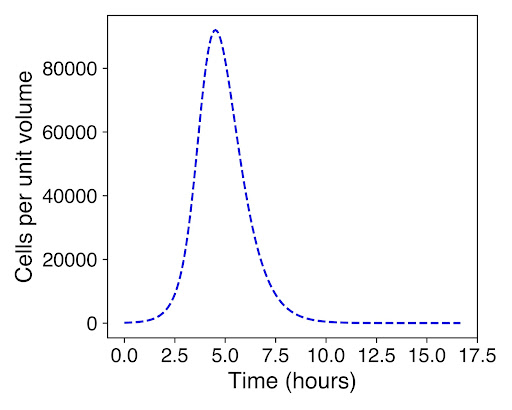
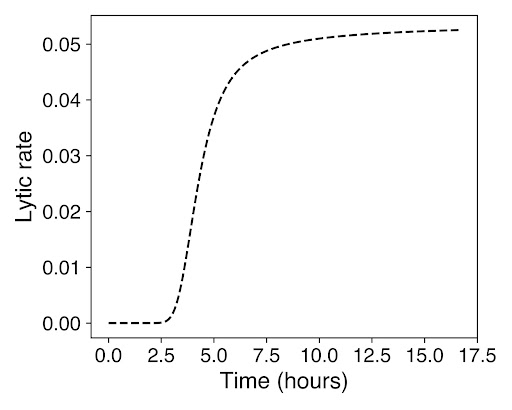
As seen in the above graphs, there is a much larger growth of cells before lysis occurs, demonstrated that our prediction of quorum sensing achieves the desired effect of having a high number of cells growing within the droplets before they all lyse. This is important to ensure that there is a high enough concentration of biosensor from the E.coli in the cells.
Furthermore, using our model, we were able to determine the relationship of the cell density before lysis occurs based on differing levels of LuxI activity, as shown in the following figure:
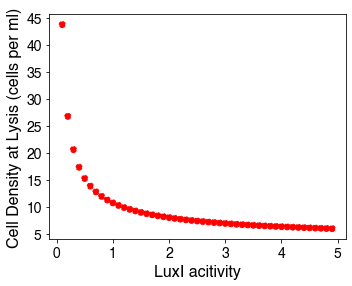
Through this result, we see that if we have a low LuxI activity, we are able to have higher concentration of bacteria within the protocell before lysis occurs. This matches intuition as lower activities cause a delay in the positive feedback circuit, leading to more cells growing before the lysis switch occurs. This modeling serves as an important result for future directions: as we design the LuxI system, we can choose reduced activities of LuxI (by choosing low activity ribosome binding sites) to achieve a high concentration of cells within the droplet, which would allow us to have high concentration of biosensor for sensitive detection schemes.